Multi-View, Radar-Based shape and reflectivity reconstruction in remote sensing using PDE-based methods (active surfaces and level set method)
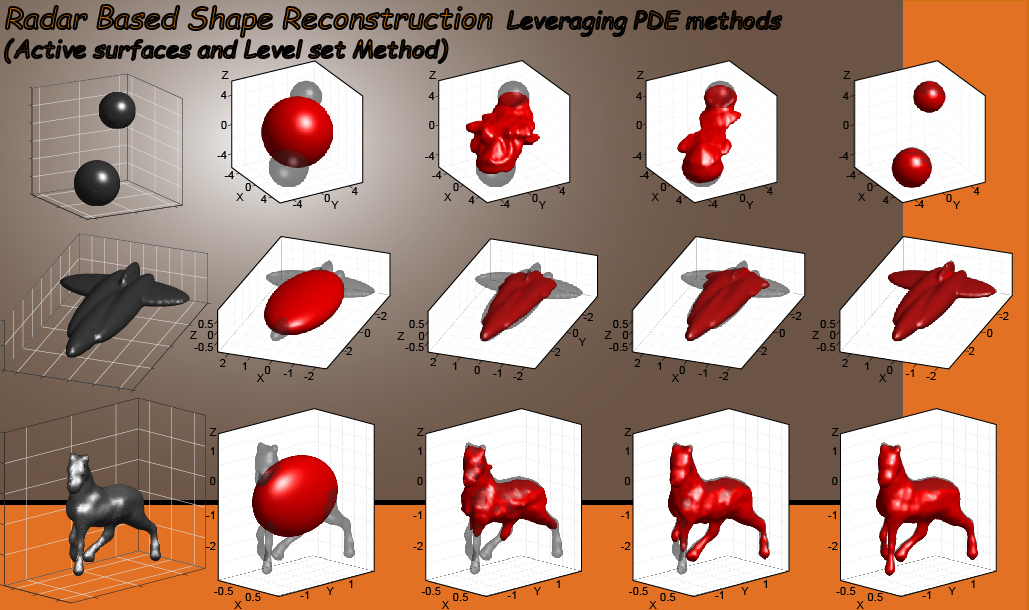
- Radar-based reconstruction: Video-1 (Two Spheres) Video 2 (Airplane), Video 3 (Horse)
This page concerns the main research topic I have been investigating since May 2017, when the Georgia Institute of Technology (GaTech) recruited me to work on the problem and join the Electrical and Computer Engineering (ECE) department with Prof. Anthony J. Yezzi.
The challenge is the reconstruction of the three-dimensional shape of the investigated scene (and the reflectivity defined on it), from a set of radar echoes (i.e. complex-valued time series), recorded independently at sparse locations.
We tackle the problem of shape reconstruction using a PDE-based approach. In practice, we leverage an active surface, described implicitly through a level set function, which is evolved from an initial (wrong) shape toward the shape whose simulated response best reproduces the recorded data.
The mathematical method employed has a close connection with the research I conducted during a previous postdoctoral appointment in 2014 at GaTech, except that in 2014 I investigated the use of active surfaces and the level set methods for the detection and geometrical description of inclusions or defects in solids based on elastic wave measurements. While active surfaces are very popular in computer vision, their use in connection with radar signals for remote sensing and shape reconstruction is completely new.
The main products of most modern radar techniques are high-resolution images. Among the many existing approaches to image formation, the Synthetic aperture radar (SAR) is perhaps the best example of this entire class of applications. SAR leverages a moving antenna, emitting pulses at regular intervals to illuminate the scene from multiple viewpoints. In particular, in spotlight mode SAR, the antenna is moved along a linear or circular trajectory while the beam is steered to point toward the scene. Data collected at the antenna are complex-valued time series which are then assembled into a two-dimensional dataset. One dimension is delay time (or two-way pulse travel time), while the second dimension corresponds to the antenna path. Information within this raw data is entangled in a complicated way, nevertheless, signal processing techniques, although involved, are sufficient to achieve the final image products. Methods to retrieve the 3D shape of the scene do exist, but ultimately, shape reconstruction from radar has typically relied on applying post-processing computer vision and/or image processing techniques, originally designed for optical images, to radar imaging products.
A key operation in image formation is coherent summation, which becomes challenging as the frequency band of the emitted signal increases.
Furthermore, the geometry of acquisition is typically limited to simple configurations such as straight or circular paths.
In contrast, by leveraging a framework very similar to the multi-view stereo reconstruction commonly used in computer vision we cast the problem in form of inversion with the ultimate goal of evolving an active surface. Inversion has seldom been applied to radar because any Energy (the functional to minimize during the iterative inversion process), built out of oscillating signals (radar echoes are highly oscillating), is bound to contain a large number of local minima. Local minima are well known for making inversion very difficult, if possible at all. We were able to establish a preprocessing method to avoid this particular issue, therefore obtaining a well-behaved energy.
Applications: Main applications of this research may be anticipated in the fields of remote sensing and data fusion, robotics, and unmanned vehicles. We engineered a mathematical very similar to the image-based multi-view stereo reconstruction, except for the fact that here the shape reconstruction is achieved by the inversion of radar echoes (not images). While this is still ongoing research, far from reaching its true potential, our approach presents several desirable properties: 1) we created a framework where, in the future, it will be natural to fuse optical images (and other modalities as well), with radar. 2) our approach does not suffer from the high-frequency limitations of radar imaging. 3) the approach naturally handles sparse antenna locations.
In the following, I provide a few simulated examples of reconstruction in full 3D which demonstrate our most recent results using active surfaces (Bignardi et al. 2021).
- Video 1. Reconstruction of two spheres, showing the method can handle topological changes
- Video 2. Reconstruction of an airplane-like silhouette.
- Video 3. Reconstruction of a horse-like shape, showing that our method can handle complex shapes.
Our latest implementation using active surfaces builds upon and expands the general framework we detailed in (Bignardi et al. 2020) which considered the simpler case of a surface described as the graph of a function. An example of our former results can be found here: Graph of a function approach.
I believe this research is very promising, especially because practical applications at different scales can be conceived.
1. SAR: Synthetic Aperture Radar
2. PDE: Partial Differential Equation