S3D/S3Di (Acoustic/Elastic 3D propagation and Full Waveform Inversion)
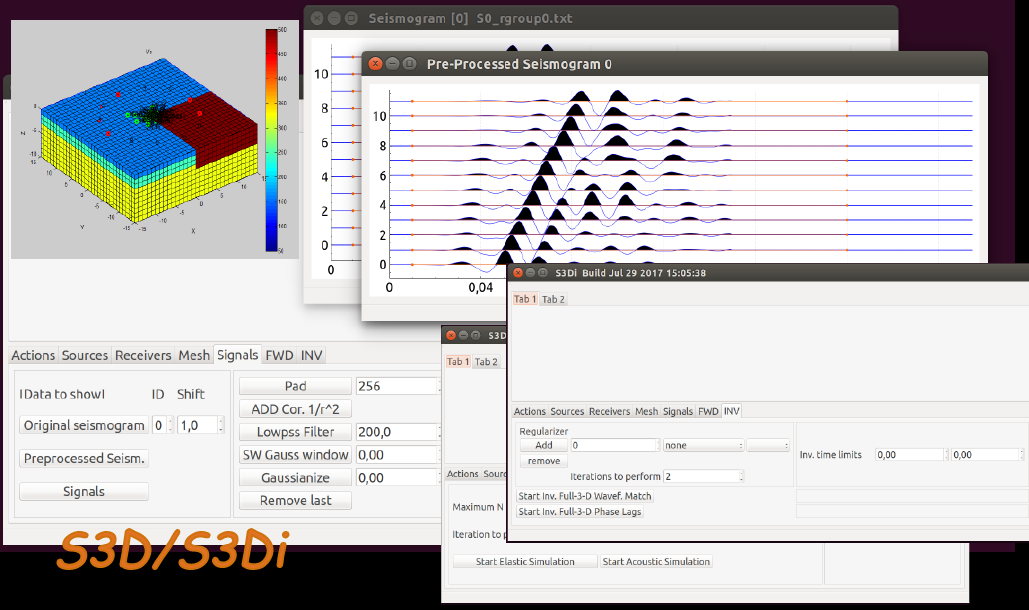
S3Di is a computer program developed in C++ and dedicated to acoustic and elastic propagation (in time-domain) of waves in solids.
I created the program for research purposes. Until now the code is not available.
A graphical user interface (GUI), developed using QT is used to interact with two core routines:
Simulation (Forward model).
The routine can simulate both the purely acoustic and the elastic wavefield propagation in a general subsurface and/or trough geometrically complex objects. The wave propagation simulator implements the time-marching Spectral Finite element Method. Inspired by Komatitsch's, Vilotte's and Trump's work (1998,1999), I re-derived the mathematical formulation of the elastodynamic problem and created my own C++ implementation (i.e. the code is a fresh implementation and not a porting). Accuracy of the result was verified against the program "SPECFEM3D", developed in fortran by Komatitsch, Vilotte and Tromp.
Input to the program is provided by a set of ascii files, while the geometry of the mesh can be generated either using CUBIT, or a purposely developed graphical Matlab tool. If cubit is used, the geometry can be very flexible, opening a wide range of opportunities for application of the present program in fields such as engineering, mechanics and geotechnics. Concerning the graphical Matlab tool, it comprises the visualization of the the produced model in 3D, investigation of the properties of sources and receivers, and implements a graphical tool for the evaluation of the stability condition of the spectral element method with respect to the spectral properties of the source's signal (exciting force). The latter capability, to my knowledge, is not available in any code.
Inversion
Inversion of the wavefield is implemented in form of local optimization. As in most local methods, a cost functional is iteratively minimized while evolving the parameters describing subsurface/object (the model), from an initial guess toward an optimized version.
The gradient of cost function with respect to a changes in the model parameters is computed via the Adjoint method, while the optimal parameters change is computed trough the conjugate gradient descent method.
Some implementation details are worth to mention: typically, to obtain the gradient of the energy functional using the Adjoint method, the propagated (forward) wavefeld and the corresponding adjoint field are computed; their product is then integrated over space and time. The sources of the adjoint field are typically located at the receivers locations of the forward wavefield and their temporal variation is dominated by the mathematical form of the energy functional. The adjoint field is computed by propagating the effect of the adjoint sources backward in time. The main advantage of this approach is that in order to obtain the energy gradient, only two runs of the forward model are sufficient.
While detailes fo the adjoint method can be found in Plessix (2006), it is important to highlight that the computation of the energy gradient requires to store in memory (or on disk), the values of displacement, velocity, and acceleration of both wavefields for each node of the mesh, each component of motion, and each time sample. The memory demand quickly grows prohibitive for most desktop or laptop computers.
Therefore, I implemented the inversion routine so that a first execution of the forward model is used to record the propagation wave field status at specific time intervals. Subsequently, the forward and backward propagation are piecewise computed for finite portions of time. The main advantage of this strategy is that the RAM necessary to the computation is nearly two order of magnitude lower, at the only cost of one extra run of the forward model. Consequently, during each iteration adjoint forces are computed dynamically, without the need of saving it into large data on file and pausing the algorithm when they are reload in. Further, despite the currently implemented inversion approach is based on a Least squared Full waveform inversion-style (FWI), the form of energy functional to minimize, and therefore, the inversion approach, can be easily customized by simply substituting the dedicated computational routines.
Future development:
- work is in progress to develop a 2D version of the code. The motivation is because the full 3D computation is unpractical when the subsurface to model is large, e.g. for applications in exploration geophysics.
- research is in progress for small-scale geotechnical application, e.g. soil-structure interaction, and evaluation of the effects of soil compaction interventions.
References
2006: Plessix, R.E., A review of the adjoint-state method for computing the gradient of a functional with geophysical applications. Geophysical Journal International, 167, p. 495–503, DOI: 10.1111/j.1365-246X.2006.02978.x
1999: Dimitri Komatitsch and Jeroen Tromp, Introduction to the spectral-element method for 3-D seismic wave propagation, Geophysical Journal International, 139, p. 806-822
1998: Dimitri Komatitsch and Jean-Pierre Vilotte, The Spectral Element method: an efficient tool to simulate the seismic response of 2D and 3D geological structures, Bulletin of the Seismological Society of America, 88, p. 368-392